Polonaise inverse
Il y a un peu plus de trente ans, HP sortait sa première calculatrice, une machine restée célèbre pour son utilisation de la notation polonaise inverse. J’ai fait toutes mes études avec une HP28C. Non seulement j’ai toujours trouvé ce système de notation plus pratique et moins ambigu que le système classique, à tel point que je suis quasiment incapable d’utiliser une calculatrice normale ; mais de plus, l’avantage d’avoir une HP sur les bancs de la fac, c’est que personne ne vous emmerde à vouloir vous emprunter votre calculatrice !
Pour comprendre comment fonctionne la notation polonaise inverse, il faut voir les formules mathématiques comme un arbre. Les nœuds (en couleur ci-dessous) sont les opérations à effectuer : addition, multiplication, sinus, logarithme, élévation au carré, etc. Tandis que les feuilles (en blanc ci-dessous) sont les opérandes, soit des nombres, soit des constantes prédéfinies dans la machine comme π ou e. Imaginons que vous ayez à calculer le résultat de 2 + 3 sin (17 + π). Cela peut se représenter par l’arbre suivant :
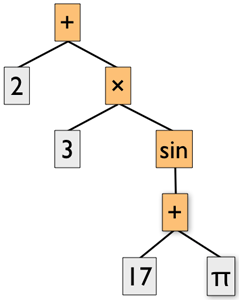
Il existe plusieurs façons d’énumérer tous les nœuds d’un arbre. Une méthode intéressante est de le parcourir en profondeur, ce qui consiste à descendre le plus possible chaque fois qu’un chemin se présente à gauche, puis quand ça n’est plus possible, chaque fois qu’un chemin se présente à droite. C’est en remontant qu’on énumère alors les nœuds. Dans cet exemple, on obtient 2, puis 3, puis 17, puis π, puis +, sinus, × et enfin +. Ce parcours s’obtient aisément en appelant la fonction récursive suivante sur la racine :
visiter_noeud(x)
{
si x possède un fils gauche,
alors visiter_noeud(fils_gauche(x))
si x possède un fils droit,
alors visiter_noeud(fils_droit(x))
imprimer x
}
Dans un tel parcours en profondeur, il y a trois options possibles : le parcours préfixe, le parcours infixe, et le parcours postfixe. La différence réside dans le moment où l’on imprime le nœud courant, c’est-à-dire l’endroit où se trouve l’instruction « imprimer x » dans le code ci-dessus. Pour le parcours préfixe, on imprime le nœud courant avant de visiter les fils. Ce cas ne nous intéresse pas ici. Dans le parcours infixe, on imprime le nœud courant entre la visite du fils gauche et la visite du fils droit. Avec notre exemple, on obtient : 2, +, 3, ×, sinus, 17, +, π. Autrement dit, on obtient exactement la formule de départ. Enfin, dans le parcours postfixe, on imprime le nœud courant après avoir visité les deux fils. C’est ce que fait le code ci-dessus. Avec notre exemple, on obtient : 2, puis 3, puis 17, π, +, sinus, ×, et enfin +. Eh bien vous savez quoi ? Cet ordre est exactement l’ordre dans lequel il faut appuyer sur les touches d’une calculatrice HP pour effectuer l’opération !
Résumons : toute formule mathématique peut être représentée de façon unique et non ambiguë par un arbre. Sur une calculatrice classique, on effectue le calcul en entrant la formule dans l’ordre donné par un parcours infixe de cet arbre. Sur une calculatrice HP, on l’effectue en entrant la formule dans l’ordre donné par un parcours postfixe. C’est aussi simple que ça.
Pourquoi cette dernière façon de faire est-elle préférable à mon sens ? Parce qu’il n’y a aucune ambiguité sur la priorité des opérateurs. Dans la notation infixe, pour que ça marche, il faut que la calculatrice et l’utilisateur s’accordent sur le fait que la multiplication est prioritaire devant l’addition. Sinon, le résultat produit est faux, à moins de permuter certains fils gauches et droits pour que les opérations se fassent dans le bon ordre. Or certaines calculatrices n’utilisent pas les priorités usuelles – c’est typiquement le cas des calculatrices de bureau bon marché et des applications écrites à la va-vite. Autrement dit, si vous entrez la même opération sur deux calculatrices différentes, vous pouvez obtenir un résultat différent. La preuve ? Prenez un MacBook. Sur l’application Calculatrice, tapez 2 + 3 × 4. Vous obtiendrez 14. Prenez maintenant le widget calculatrice qui se trouve sur le dashboard et tapez exactement la même opération. Vous obtiendrez 20. Plutôt ennuyeux, non ?
Dans la notation postfixe utilisée par les calculatrices HP, ce problème n’existe pas. Les opérations sont forcément entrées dans le bon ordre. Vous n’avez pas à vous demander si la priorité naturelle des opérateurs est prise en compte ou non, vous n’avez pas à vous demander dans quel ordre la machine va faire les opérations, parce que cette notion de priorité n’a pas de sens. C’est aussi pour ça qu’il n’y a pas de touches parenthèses sur une calculatrice HP : elles ne serviraient à rien.
Pour finir, un petit exercice classique que je donnais habituellement à mes stagiaires à une certaine époque : écrire un programme qui convertit une formule mathématique depuis la notation infixe vers la notation postfixe. Le B.A.BA quand on prétend travailler sur l’écriture de compilateurs ! La solution : construire l’arbre à partir de la notation infixe en utilisant un analyseur syntaxique généré par un script YACC, puis utiliser une fonction récursive telle que celle donnée ci-dessus pour réaliser un parcours postfixe en profondeur de cet arbre.